(Data Structure) Linked List

연결 리스트(LinkedList)란?

 각 자료를 동적 할당으로 따로 잡아주고 이러한 자료들을 하나로 묶어 순차적으로 관리할 수 있게 리스트화 한 것이 다. 

연결 리스트 종류
1. 단일 연결 리스트(single Linked List)
2. 더블 연결 리스트(Dubble Linked List)
3. 원형 연결 리스트(Circular Linked List)

 

※single Linked List

• 리스트가 한 방향으로 이루어져 있다. (각 노드는 다음 노드의 주소만 안다.)
• 각 노드의 데이터는 무슨값이든 될 수 있다. data가 무엇이든지 typedef선언으로 변경해주고 조금의 수정만 하면, 사용 가능하게 구현되어야 한다.

단일 연결 리스트는 위와 같은 구조로 이뤄져있다.

• 단일 방향이기 때문에 특정 방향으로만 타고 들어가 모든 정보를 찾아갈 수 있다.
• 리스트의 첫 시작 부분의 기준이 되는 노드: head
• 리스트의 끝 부분의 기준이 되는 노드 : tail
• 리스트의 기준이 되는 노드인 head, tail은 리스트의 종류에 따라 둘 중에 하나가 빠질 수 있다. 
• 위의 그림은 head를 기준으로 Node *next를 통해 다음 자료형을 참조한다. 

## 장단점

장점 

• 새로운 노드의 추가, 삽입, 삭제가 쉽고 빠르다.

단점 

• 특정 위치에 있는 노드를 검색하는데 속도가 느리다. (n개의 자료형의 빅오 : O(n) )  
• 한 방향으로만 검색이 가능하다.

 
##방식
1. head를 더미 노드로 선언하는 방식과 더미 노드를 안 쓰는 방식

2. head에 추가하는 방식

3. tail에 추가하는 방식

##코드 영역에서 살펴보기
코드 영역은 head와 tail을 둘 다 이용하는 형태인 연결 리스트 Queue를 기준으로 설명하고, stack에 대해서도 간단히 설명하겠다.

노드 선언 형태가 단순 연결 리스트 구조체 선언
  

Front == head, rear == tail이다.
Queue는 FIFO(FirstInFirstOut) 구조이다. 따라서 Queue는 데이터 삽입시 rear증가, 데이터 삭제 시 front 증가로 연결 리스트를 설명하기 좋은 자료구조이다. 

QueueList 선언

아무런 데이터 삽입이 되지 않아서 front와 rear 둘 다 NULL이다. (더미 노드 NO사용)
데이터 삽입 함수 (코드 설명은 주석처리)

데이터 삭제 함수

이외에도 출력 함수, 참조 함수, 비었는지 체크하는 함수, 데이터 개수 파악 함수 등을 만들 수 있지만 리스트의 정의만을 설명할 것이므로 따로 언급을 하진 않겠다.

(참조 함수는 중요하므로 Double Linked List에서 보임)



Stack code 
 - stack code는 위에서 단방향 연결 리스트에 대해서 함수를 통해 정리하였으니 코드를 활용하여 stack에서 연결 리스트가 어떻게 쓰이는지만 보여주겠다.
 Stack은 LIFO(Last In First Out) 구조로서 Top 포인터만 존재한다. 그래서 연결 리스트에서는 Head만을 활용하여 머리에 추가하는 방식을 쓴다.

코드 영역

Stack Node 구조체 선언 및 top 포인터 선언

top포인터가 전역에 선언되었기 때문에 , 함수의 parameter로 List를 줄 필요가 없다.
top은 List이자 node가 된다. Insert함수에서 설명하겠다.


삽입 함수(Push)

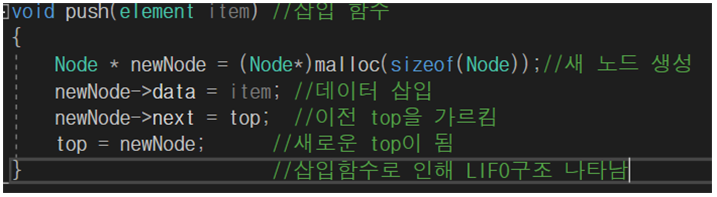
삽입 설명 

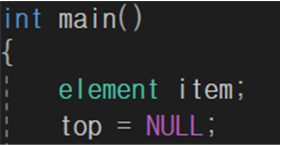
 위를 보면, top초기값을 NULL로 해줌으로써 NULL top 초기값을 가리킨다.

 push를 하게 되면 new node가 생성되고 new node가 top을 가리킨 후, new node는 새로운 top이 된다.

 그리고 초기 삽입 이후에도 똑같은 형태가 반복된다.

즉, 위 그림과 같은 눈에 List라고는 나오지 않지만 next pointer로 연결이 된다. 따라서 top은 node이자 list자체가 된다! 

또한 머리에 node를 추가하는 방식으로 LIFO구조가 완성된다.

 

꺼내는 함수(pop, 삭제 함수)
 

IsEmpty() 함수

pop함수에서 사용된 IsEmpty함수 쉽게 이해할 수 있다.
비었을 때 pop함수를 호출하면, Stack is empty!라는 문자열  출력 후 프로그램을 강제 종료시킨다. 

왜냐하면 잘못된 메모리 구간을 건들기 때문이다.

 

main함수

print함수는 굳이 설명하지 않겠다.

 

결과창

stack의 상태 표현

여기까지 stack의 연결 리스트 활용에 대한 코드의 설명을 마치겠다. stack과 queue는 자료구조이다. stack을 활용하여 infix방식을 postfix로 구현하거나(수식 Tree 표현) Queue를 이용하여 가게의 대기 손님 simulation 같은 프로그램 등에 활용할 수 있다. 

※Double Linked List

 -노드가 전 노드와 다음 노드의 주소를 알고 있다.

• 이전 주소와 다음 주소를 알고 있기 때문에 단일 연결 리스트보다 원하는 데이터를 참조하기가 편하다.
• 단순 연결 리스트의 확장 버전이다.
• 단순 연결 리스트보다 prev인자를 하나 더 선언하기 때문에 메모리를 더 소비한다.
  
  

코드 영역 보기
이번 코드 예제는 tail이 없어지고 head에 추가하는 방식이다. 

더블 연결 리스트의 구조체 node선언, List선언

 단일 연결 리스트와 다르게 data 수를 선언해줬음

삽입 함수 

:새 노드를 머리에 추가

참조 함수 : 이곳에서 list인자 Node * cur 사용된다.
처음 호출되는 함수 

LFrist 이후에 호출 가능한 함수 

Lfirst와 LNext가 나눠진 이유는 현재 위치를 나타내는 cur노드가 다시 head로 돌아가는 시점이 애매하다. 

그래서 Lfirst가 cur = head로 만들어주는 함수이다. 그래서 LNext는 LFirst이후에 선언 가능하다.

이전 노드 참조 함수

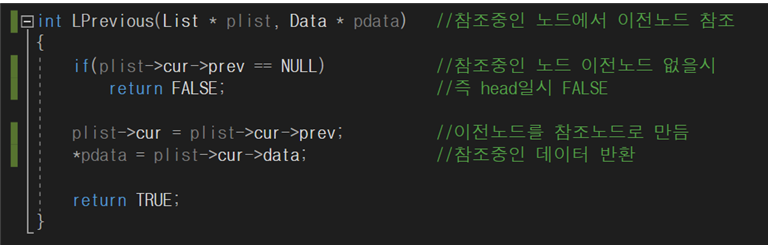
LPrevious함수도 LFirst이후에 실행 가능하고, 이전 노드를 참조하는 함수이다.
LPrevious함수도 보여주기 위해서 양방향 함수에서 참조 함수를 보여주었다.

메인에서 참조 함수가 쓰이는 방식

※Circular Linked List

-원형 연결 리스트는 단방향 연결 리스트나 더블 연결 리스트에서 처음 값과 이전 값을 연결한 리스트이다.

이중원형리스트의 예제

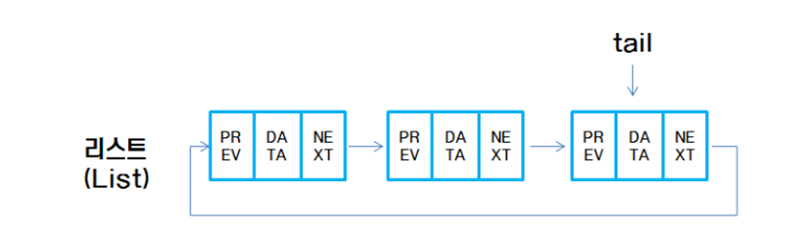
• 위 그림을 보면 node변수가 head가 아닌 tail만 존재한다. 왜냐하면 tail을 이용하면 끝 노드와 처음 노드를 모두 참조할 수 있기 때문이다.  (물론 head도 사용 가능하다. 하지만 tail만 사용하는 것이 편리하다.)
  Ex) 첫 노드 참조 : list->tail->next; 끝 노드 참조 : list -> tail;
• 이중원형 연결 리스트를 사용하면 원하는 노드를 참조하는 것이 빠르다. 왜냐하면 만약 끝과 가까우면 끝에서부터 prev로 찾아가면 되고, 처음과 가까우면 tail->next부터 next로 찾아가면 되기 때문이다.
  
  

코드 영역
-Insert와 Delete, 참조, 이전 노드 참조 함수를 위에서 전부 보였다. 원형 연결 리스트라고 해서 원래의 틀에서 크게 벗어나지 않고 함수의 역할이 모두 똑같다. 함수의 내용의 10% 정도만 달라질 수 있다. 여기서는 끝에 Insert 하는 것과 처음에 Insert하는 것을 보여주겠다.

구조체 선언&리스트 선언

꼬리에 삽입 함수 

다소 코드가 길어진 이유는 이중원형 연결 리스트로서 위에서 보인 모든 insert기능이 다 포함되어있기 때문이다. 이전 노드와 다음 노드의 참조 구간을 모두 다루기 때문이다.


머리에 삽입 함수

사실 이 함수는 꼬리 추가 방식에서 코드상으로는 한 줄만 줄은 것이다. 그래서 굳이 왜 나누어 두었나 생각이 들 수도 있다. 하지만 그 한 줄 코드인 plist->tail = newnode; 가 있냐 없냐에 따라서, 누가 tail이 되냐, 즉 기준점이 되냐가 갈리기 때문에 중요하다.




마지막으로 연결 리스트의 활용인 Polynominals를 소개하겠다.
연결리스트의 활용 자료로 Polynominals를 선택한 이유
 -위에서는 연결 리스트를 여러 개사용하는 것은 소개하지 않아서이다. 또한 연결리스트를 여러 개 선언하여 활용하는 Polynominals를 소개하면 노드를 연결하고 끊는 방식에 대해 잘 이해할 것 같아서 선택하였다. 

(위는 아주대학교 김강석 교수님의 Data Structure 수업 자료를 활용)
C(x) = A(x) + B(x)를 연결 리스트를 활용하여 짜는 코드이다.
즉 각각의 x^n이 하나의 노드가 되는 것이다.

코드 영역

List 구조체와 Node구조체 선언  , List 초기화 함수

삽입 함수(다항식의 tail에 추가)

주석처리로 써놓았지만, 만약 tail에 추가 방식이 아닌 중간에 삽입하고 싶은 경우는
위에서 설명한 참조 함수를 활용하여 expon을 비교하여서 삽입하면 되겠다.
이건 C(x)를 만드는 과정에서 나타난다. (위에서 설명한 참조 함수가 아닌 A(x)와 B(x)의 expon 비교; 원리는 같다) 

덧셈 함수(C(x) 구성 함수)  -> A(x)와 B(x)의 최고차 항부터 승수 비교 승수 높은 node 삽입

 

A(x)의 승수가 클 시

B(x)의 승수가 클 시

주석처리를 안 한 이유는 A(x)의 승수가 클 시와 원리 같음

A(x) 승수 == B(x) 승수

계수의 합이 0이면 A(x)와 B(x)의 다음항을 참조하게 하고 계수의 합이 0이 아니면 삽입 원리 같다.

다음으로 A(x)나 B(x)둘 중 하나가 끝에 도달했을 때 

main함수

 

결과창

이것으로 Polynominals의 설명을 마치겠다.




마무리하며..
 이렇게 연결 리스트에 대하여 개념과 코드를 보여주면서 정리해보았다. 과제를 하면서 내가 짰었던 코드를 다시 보는 계기가 되었다. 그래서 꼭 알고 가야 하는 개념임을 다시 한번 remind 하는 계기가 되었다. 연결 리스는 stack, queue, deque, tree 등 너무 많은 것들의 기반이 된다. 절대 잊지 않도록 계속 활용해야겠다.